Defining Batting Consistency Through Clusters
What can computational cosmology teach us about batting?
Three years ago, I was working on computer simulations of baby universes. One of the ubiquitous computational tools we use in analysing the results of these simulations is called the “Friends-of-Friends” algorithm. We simulate the motion of dark matter in these, and the ultimate objective is to find clusters of dark matter (which is amenable to clumping together on very large scales in the universe). The FoF method looks for clusters of matter by grouping together particles that are close enough in space.
This gave me an idea: why not find similar clusters of good batting using this algorithm on a player’s career? After all, our casual definition of batting consistency is “does the batsman score high enough often enough”.
My latest article for ESPNcricinfo is a culmination of this idea. The aim is to check how much of a career is covered in such clusters. Players who are in these phases of scoring highly often enough are more “consistent”.
I hope you enjoy this article. It’s been one of my favourite projects, and I have mulled over it for such a long time. The graphics have taken some effort to make, but I’m happy with how they have turned out (thanks to Matplotlib, the python plotting library).
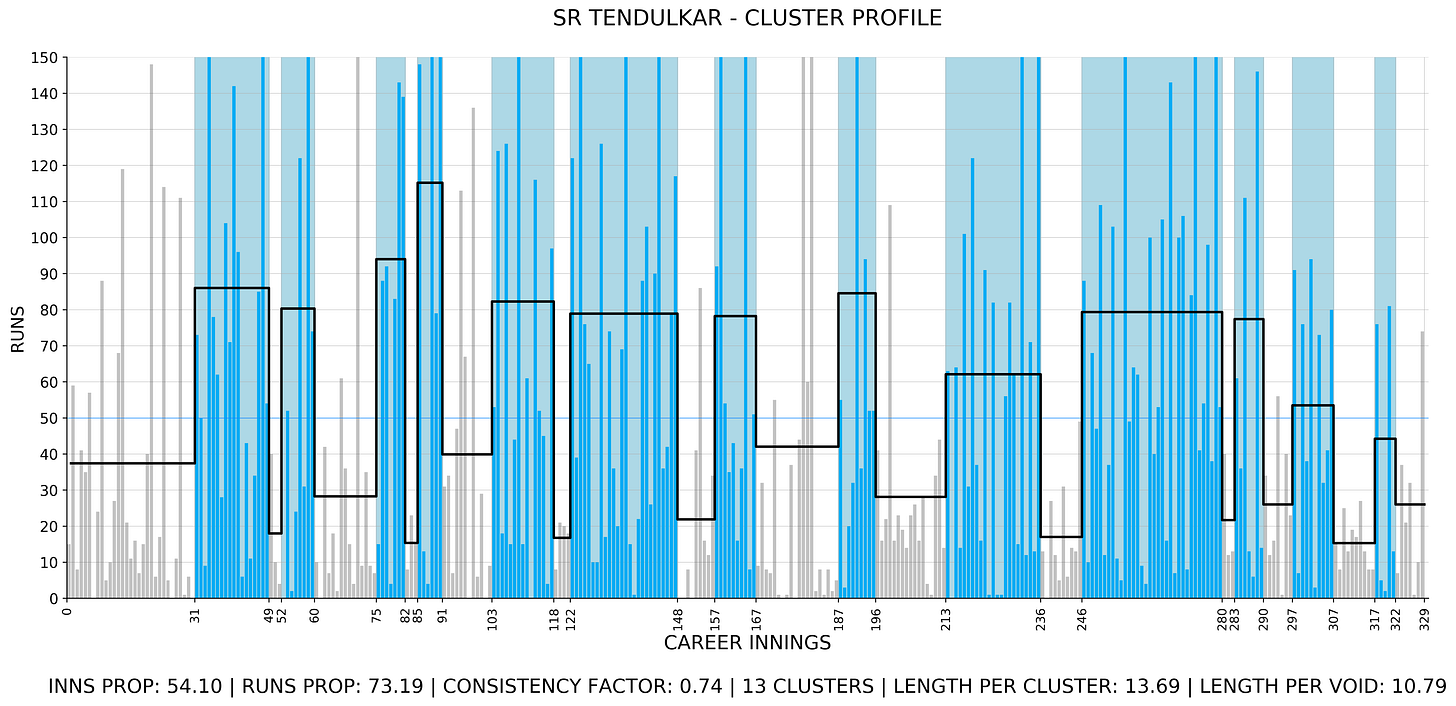
This is Tendulkar’s career with a “gap” of 3 innings, and a threshold of 50, which means a cluster is broken if he has a gap of 3 or more between consecutive 50s.
There are 6 important numbers here:
Proportion of innings covered in clusters.
Proportion of runs covered in clusters.
The ratio of 1 to 2: this tells you how evenly high scoring the player has been.
No of clusters.
Length per cluster on average: how long are the good streaks.
Length per void on average.
Other two numbers of importance are the runs per inns in clusters and voids, which tell you how good or bad a player is in his good or bad phases.
This contains the cluster plots for all batsmen with 5000 or more Test runs.
This file has the various numbers for all these players.