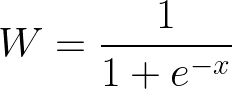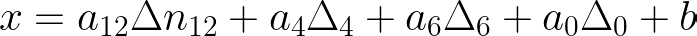A few months ago, I had a slew of ideas ready to put into words and figures for ESPNcricinfo, but they were mostly to do with Test cricket. As it was IPL time, I was asked if I had something on T20. I’d had ideas, but never really given them much thought. This was a good reason to start.
As a result, I have now written three articles for ESPNcricinfo, trying to answer different kinds of questions about T20. The format is still new and in the clutches of cricketing convention, slowly breaking out as its own game. Many questions remained unexplored, even unasked. This is my attempt at looking at T20 through some numbers.
A few concepts and results might be familiar to the reader of this newsletter already. I will mainly explain the methods of the 3rd article in detail below, for those interested. Then, I will talk a bit about the first two pieces.
How important are boundaries in T20?
It has been known for a while in online circles of analysts, and within team managements, that boundaries are the currency of T20. Singles and dots are given too much importance in mainstream commentary, which borrows from the language of cricket, as opposed to talking in terms of T20.
I wanted to quantify how much more valuable boundaries really are compared to dots and singles etc. I used a logistic regression model for this, which modelled the match result with logit.
Where Δn is the difference in the number of that kind of scoring shot between the two teams. x is the logarithm of the odds of winning (called log-odds). I used a logistic regression and data from matches from IPL, CPL, BBL and PSL to find the best fit coefficients. The interpretation of each value of a is that exp(a) is the factor by which the odds get multiplied for each unit increase in the corresponding Δn. So, hitting an additional four would increase your odds exp(a_4) times.
This model fit well, with a pseudo-R^2 of 0.71.
Moreover, the ratio of any two coefficients gives you the relative value of those two kinds of scoring shots. Think of it this way: if you hit one extra dot, your log-odds would change (decrease) by a_0. To maintain the same odds, how many extra sixes would you need to hit? a_0/a_6.
The article first lists the odds ratios and relative worth of a dot in terms of 6s and 4s. I found it interesting that when I fit data from individual leagues, 1s/2s had no significant relationship to the response at the 0.95 sig level.
I wanted this to be a general exploration of boundary hitting. Watching the IPL, the strategy of elite hitters struck me as “always looking for boundaries”. I began to think of boundary hitting as a binomial process: you try hitting a boundary independent of the situation. What would happen if teams just attempted to hit more boundaries? I began thinking of run targets in terms of sixes. 80 from 30 was actually “can 10 sixes be hit in 30 balls?” Why not? Can an elite hitter have a success rate of 33%?
To my disappointment, no one records “boundary attempted” data as a binary variable. Imran Khan from CricViz responded to my tweet about this with an excellent piece he’d written, using the shots with the highest boundary % as a proxy for boundary attempts. I decided to use that method (which covered 85% of actual boundaries hit), and Imran (and CricViz) were kind enough to give me some data. I needed the actual distribution of outcomes when people attempted to hit boundaries vs when they didn’t.
The results are clear: trying to hit boundaries gives you a much higher run payoff, even if the dismissal rate goes to 11% (from 2% on balls you don’t attack). A team deciding to attack all 120 balls would get all out many times, but also have higher totals than most other teams. More results are in the article.
The way to really test this was to run Monte Carlo simulations of these scenarios. The idea is that the number of balls attacked is a controllable for the batting side. It’s a knob you can turn to analyse the outcomes of a variety of strategies.
Let’s take a scenario. 10 overs left, 5 wkts in hand, 100 to get. Let’s decide to attack 40 balls out of 60. Then, the attack probability is 0.67 (40/60).
I loop over 60 balls. On each ball, I can decide to attack with a chance of 0.67. Depending on that choice, I sample from the distribution of outcomes I have at hand (remember, these are two different distributions, depending on attack / not attack status).
I simulate all 60 balls this way. I check the total wickets. If W >= 5, I take the portion of the 60 balls until 5 wickets fall. If not, I take all 60 balls. I then sum up the runs scored. If this is 80 or more, the team has won.
I run this very simulation 10000 times and record the mean win percentage.
Now, change the number of balls you want to attack. Repeat.
The article explores different situations, and different kinds of players, looking for an optimal attack proportion in order to win a game or to set the best first innings total.
How do chasing teams go about their business?
I was curious about the template of the median chasing team that wins an IPL game. Do they trail behind the required rate at the beginning? When do they start to go aggressive?
My first piece tries to answer this, and more. I found that the median successful chase, to my surprise, tracks the asking rate at all points in the innings. I also show win probability as a function of runs needed in the last few overs, using a logistic regression model.
Can player contributions be translated into wins for the team?
The genesis of the methods in this article was Karthik Krishnaswamy’s article asking if an anchor is really needed in T20. His general point was lost in online cacophony as bloodthirsty cultist “fans” attacked the criticism of Kohli’s slow, suboptimal scoring in T20.
My Runs Above Average measure sought to quantify the runs scored in comparison with the average player over a season. This was to answer the question: do Kohli’s big innings make up for his slow starts and poor innings over the season? In conclusion, Kohli was found to be nearly average overall, and below average in many seasons.
This further led me investigate the relationship between team run rates and win percentages over a season. And from there, I could translate each player’s individual contribution, using RAA, into a Wins Above Average number, which is how many wins they contribute more than the average player over a 14-match typical league season.
Here is the piece.